Triangle Inequality Theorem
The Triangle Inequality Theorem states that the lengths of any two sides of a triangle sum to a length greater than the third leg. This gives us the ability to predict how long a third side of a triangle could be, given the lengths of the other two sides.
Example: Two sides of a triangle have measures 9 and 11. Find the possible range for the third side.
Solution: Let’s call the third side \(x\). Then, by the triangle inequality theorem, we have the following three true statements.
\(x + 9 > 11\)
\(x + 11 > 9\)
\(9 + 11 > x\)
These three statements come from the fact that the sum of any two sides of a triangle must sum to a length greater than the length of the third leg. We solve for \(x\) in all three of the inequalities.
\(x > 2\)
\(x > - 2\)
\(20 > x\)
ALL THREE of these must be true at the same time. That is \(x > 2\) AND \(x > - 2\) AND \(x < 2\). Two of these statements can be compressed into one, though. For, if \(x > 2\) AND \(x > - 2\), we can just say that \(x > 2\), because that accounts for both of those inequalities.
Then we are left with only two statements. \(x > 2\) AND \(x < 20\), which can be written as
\(2 < x < 20\)
That is, the length of the third leg of this triangle must be between 2 and 20.
Example: Two sides of a triangle have measures 10 and 12. Find the range of possible measures for the third side.
Solution: Again, we need to formulate three inequalities. By the triangle inequality theorem, we have
\(x + 10 > 12\)
\(x + 12 > 10\)
\(12 + 10 > x\)
Solving for \(x\), we have
\(x > 2\)
\(x > - 2\)
\(22 > x\)
Then, by combining these three statements, we obtain \(2 < x < 22\).
Below you can download some free math worksheets and practice.
State if the three numbers can be the measures of the sides of a triangle.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
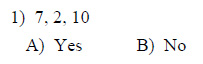
Watch below how to solve this example:
Two sides of a triangle have the following measures. Find the range of possible measures for the third side.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
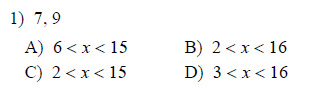
Watch below how to solve this example:
Two sides of a triangle have the following measures. Find the range of possible measures for the third side.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:

Watch below how to solve this example:


