Triangle constructions
Constructions are an important part of geometry. Architects, interior designers as well as other professions that need accurate drawings use them. You will need a ruler and a compass.
We can construct an isosceles triangle if we are given the base and the altitude. Let’s review a few vocabulary words that you will need to know in order to construct this triangle.
An isosceles triangle is a triangle with two congruent sides. The congruent sides are called legs and the non-congruent side is called the base.
The altitude of an isosceles triangle is the line drawn from the base to the opposite vertex. This line is perpendicular to the base and it bisects the base into two equal halves. The altitude of an isosceles triangle is an example of a perpendicular bisector.
Here are the steps to constructing an isosceles triangle if we are given the base and the altitude.
The Base
- Measure and draw the base with a ruler.
The Perpendicular Bisector
- Set the width of the compass to about the size of the base (the width doesn’t matter so much as long as it does not change during this step)
- Put the point of the compass on one endpoint of the base and use the pencil side to draw a small arc on the top and the bottom of the base.
- Without changing the width, repeat this step using the other endpoint of the base.
- The arcs should intersect at a point above the base and a point below the base. Using the ruler, connect these points with a straight line. Extend the line all the way through both points. This is your perpendicular bisector.
The Altitude
- Your perpendicular bisector will be longer than you need for the altitude. Measure the perpendicular bisector and erase so that it matches the length that the altitude should be.
The Isosceles Triangle
- Connect the top of the altitude to the endpoints of the base.
Congrats! You have constructed an accurate isosceles triangle!
Below you can download some free math worksheets and practice.
Construct a copy of each triangle given.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
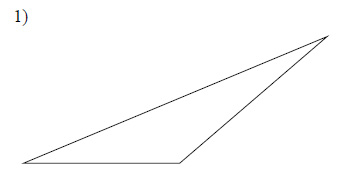
Watch below how to solve this example:
Construct an isosceles triangle given the length of the base and the length of the altitude.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
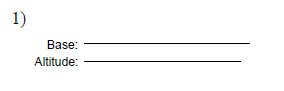
Watch below how to solve this example:
Construct a 30-60-90 triangle using the segment given as the hypotenuse.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:

Watch below how to solve this example:


