Adding and subtracting
Adding and subtracting rational expressions is similar to adding and subtracting fractions. You need a common denominator. While the method is easy, the problems can be a little complex because of the size of expressions.
When adding or subtracting any fractions or rational expressions, you can use the following formula. Let a, b, c and d be any constant, variable, or algebraic expression. Then
\(\large \frac{a}{b} + \frac{c}{d} = \frac{ad + bc}{bd}\)
In this formula, the common denominator becomes the product of the two original denominators. This is the fastest method for obtaining a common denominator, although it is not necessarily the least common denominator.
Then each numerator is simply multiplied by the denominator of the other fraction, and those results are added together.
Let’s try an example. We would like to subtract the rational expression
\(\large \frac{2b}{2b + 5} - \frac{8b}{7b + 7}\)
We can use the above formula, adjusting the sign for subtraction. Then all we need to do is simplify. The formula gives
\(\large \frac{2b}{2b + 5} - \frac{8b}{7b + 7} = \frac{(2b)(7b + 7) - (2b + 5)(8b)}{(2b + 5)(7b + 7)}\)
\(\large = \frac{14b^2 + 14b - 16b^2 - 40b}{(2b + 5)(7b + 7)}\)
\(\large = \frac{-2b^2 - 26b}{(2b + 5)(7b + 7)}\)
\(\large \frac{-2b^2 - 26b}{7(2b + 5)(b + 1)}\)
In the last step we simply factored out the common factor 7 from 7b + 7. Congratulations! You’ve successfully subtracted two rational expressions. Now let’s try another example, using the same method.
Add the rational expressions
\(\large \frac{6x}{8x} + \frac{x - 6}{x + 3}\)
Before we use the formula to add these two rational expressions, we can easily simplify the first term by cancelling the x common to both factors. We have
\(\large \frac{6x}{8x} + \frac{x - 6}{x + 3} = \frac{6}{8} + \frac{x - 6}{x + 3} = \frac{3}{4} + \frac{x - 6}{x + 3}\)
Now we are prepared to use the formula for adding fractions. We have
\(\large \frac{3}{4} + \frac{x - 6}{x + 3} = \frac{3(x + 3) + 4(x - 6)}{4(x + 3)} = \frac{3x + 9 + 4x - 24}{4(x + 3)} = \frac{7x - 15}{4(x + 3)}\)
Then our final result is
\(\large \frac{6x}{8x} + \frac{x - 6}{x + 3} = \frac{7x - 15}{4(x + 3)}\)
So we see again that we must only apply the formula for adding fractions, then complete a few simplifying steps. Be careful when adding and subtracting rational expressions. Although the method for adding these things is simple, it is easy to make a mistake because of the complexity of the expressions.
Bellow you can download some free math worksheets and practice.
Simplify each expression.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
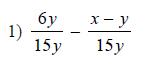
Watch below how to solve this example:
Simplify each expression.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
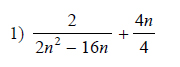
Watch below how to solve this example:
Simplify each expression.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
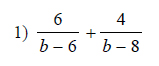
Watch below how to solve this example:


