Properties of exponents
Exponents have their own set of properties. They can seem confusing at first, but with practice we can master them just as we mastered the properties of numbers and operations. Let’s begin by stating the properties of exponents.
- Zero Exponent Property \(\Large {a^0} = 1, a \ne 0\)
- Negative Exponent Property \(\Large {a^{ - b}} = \frac{1}{{{a^b}}}, a \ne 0\)
- Product of Powers Property \(\Large {a^b} \cdot {a^c} = {a^{b + c}}, a \ne 0\)
- Quotient of Powers Property \(\Large \frac{{{a^b}}}{{{a^c}}} = {a^{b - c}}\) \(a \ne 0\)
- Power of a Product Property \(\Large {a^c} \cdot {b^c} = {\left( {ab} \right)^c}, a,b \ne 0\)
- Power of a Quotient Property \(\Large \frac{{{a^c}}}{{{b^c}}} = {\left( {\frac{a}{b}} \right)^c}, a,b \ne 0\)
- Power of a Power Property \(\Large {\left( {{a^b}} \right)^c} = {a^{bc}}\)
- Rational Exponent Property \(\Large {a^{\frac{1}{b}}} = \sqrt[b]{a}, b \ne 0\)
- \(\Large {a^{\frac{c}{b}}} = \sqrt[b]{{{a^c}}} = {\left( {\sqrt[b]{a}} \right)^c}\)
While these expressions can appear difficult, it is just a matter of identifying which property of exponents is happening in any particular problem. Let’s try an example.
Example: Simplify \( - 2{y^0} \cdot {\left( {{x^{ - 2}}{y^4}} \right)^2}\). Your answer should contain only positive exponents.
Solution: We need to carefully handle this problem one step at a time. First we consider the portion of the problem \({y^0}\).
According to the zero exponent property, \({y^0} = 1\), so we can rewrite
\( - 2{y^0} \cdot {\left( {{x^{ - 2}}{y^4}} \right)^2} = - 2\left( 1 \right){\left( {{x^{ - 2}}{y^4}} \right)^2}\)
\(= - 2{\left( {{x^{ - 2}}{y^4}} \right)^2}\)
Next let’s consider the part of the expression \({\left( {{x^{ - 2}}{y^4}} \right)^2}\). There are two ways we can handle this. We could use the negative exponent property to simplify \({x^{ - 2}}\) as \(\large \frac{1}{{{x^2}}}\). But this will introduce a fraction into the problem, and we would like to avoid fractions until we can no longer avoid them. So instead, we will utilize the Power of a Product Property (that’s the property that says \({\left( {ab} \right)^c} = {a^c}{b^c}\). Then we can simplify as
\(\begin{gathered}
- 2{y^0} \cdot {\left( {{x^{ - 2}}{y^4}} \right)^2} = - 2\left( 1 \right){\left( {{x^{ - 2}}{y^4}} \right)^2} \\
= - 2{\left( {{x^{ - 2}}{y^4}} \right)^2} \\
= - 2{\left( {{x^{ - 2}}} \right)^2}{\left( {{y^4}} \right)^2},{\text{ Power of a Product Property}} \\
\end{gathered} \)
Things are starting to look better. Now, in both of the parts of the problem that contain exponents, we can use the Power of a Power property to simplify even further. We have
\(\begin{gathered}
- 2{y^0} \cdot {\left( {{x^{ - 2}}{y^4}} \right)^2} = - 2\left( 1 \right){\left( {{x^{ - 2}}{y^4}} \right)^2} \\
= - 2{\left( {{x^{ - 2}}{y^4}} \right)^2} \\
= - 2{\left( {{x^{ - 2}}} \right)^2}{\left( {{y^4}} \right)^2} \\
= - 2\left( {{x^{ - 4}}} \right)\left( {{y^8}} \right),{\text{ Power of a Power Property}} \\
\end{gathered} \)
We have one more step. The problem requires us to have only positive exponents in our answer. So now we use the Negative Exponent Property to finish off the simplification. The following has the full solution as well as each property listed that we used.
\(\begin{gathered}
- 2{y^0} \cdot {\left( {{x^{ - 2}}{y^4}} \right)^2} = - 2\left( 1 \right){\left( {{x^{ - 2}}{y^4}} \right)^2},{\text{ Zero Exponent Property}} \\
= - 2{\left( {{x^{ - 2}}{y^4}} \right)^2} \\
= - 2{\left( {{x^{ - 2}}} \right)^2}{\left( {{y^4}} \right)^2},{\text{ Power of a Product Property}} \\
= - 2\left( {{x^{ - 4}}} \right)\left( {{y^8}} \right),{\text{ Power of a Power Property}} \\
= - 2\left( {\large \frac{1}{{{x^4}}}} \right)\left( {{y^8}} \right),{\text{ Negative Exponent Property}} = \large \frac{{ - 2{y^8}}}{{{x^4}}} \\
\end{gathered} \)
Let’s do one more example.
Example: Simplify \(2{b^2} \cdot {\left( { - 2{b^4}} \right)^{ - 2}}\)
Solution: We use the properties of exponents.
\(\begin{gathered}
2{b^2} \cdot {\left( { - 2{b^4}} \right)^{ - 2}} = 2{b^2}{\left( { - 2} \right)^{ - 2}}{\left( {{b^4}} \right)^{ - 2}},{\text{ Power of a Product Property}} \\
= 2{b^2}{\left( { - 2} \right)^{ - 2}}\left( {{b^{ - 8}}} \right),{\text{ Power of a Power Property}} \\
= 2{b^2}\left( {\large \frac{1}{{{{\left( { - 2} \right)}^2}}}} \right)\left( {\large \frac{1}{{{b^8}}}} \right),{\text{ Negative Exponent Property}} \\
= 2{b^2}\left( {\large \frac{1}{4}} \right)\left( {\large \frac{1}{{{b^8}}}} \right) \\
= \large \frac{{2{b^2}}}{{4{b^8}}} \\
= \large \frac{{{b^2}}}{{2{b^8}}} \\
= {\large \frac{{{b^{ - 6}}}}{2}},{\text{ Quotient of Powers Property}} \\
= {\large \frac{1}{{2{b^6}}}},{\text{ Negative Exponent Property}} \\
\end{gathered} \)
Below you can download some free math worksheets and practice.
Simplify. Your answer should contain only positive exponents.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch bellow how to solve this example:
Simplify. Your answer should contain only positive exponents.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
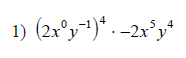
Watch bellow how to solve this example:
Simplify. Your answer should contain only positive exponents.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
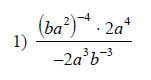
Watch bellow how to solve this example:


