Angles
Quadrilaterals are polygons with exactly four sides and four angles. One of the facts about a quadrilateral that we need to understand is that the sum of the four angles in a quadrilateral is always \(360^\circ \). That is, if you add up each of the four angles in a quadrilateral, the total measure is \(360^\circ \).
EXAMPLE: Solve for \(x\).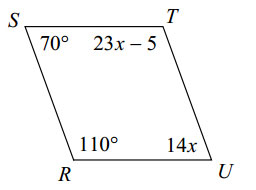
SOLUTION: The figure in this problem is a quadrilateral. Then all four of the angles in this quadrilateral will add up to \(360^\circ \). That is,
\(70^\circ + \left( {23x - 5} \right)^\circ + 110^\circ + \left( {14x} \right)^\circ = 360^\circ \)
Simplifying the left side of this equation, we obtain
\(70^\circ + \left( {23x - 5} \right)^\circ + 110^\circ + \left( {14x} \right)^\circ = 360^\circ \)
\(37x + 175^\circ = 360^\circ \)
\(37x = 185^\circ \)
\(x = 5^\circ \)
So \(x = 5^\circ \).
EXAMPLE: Solve for \(x\).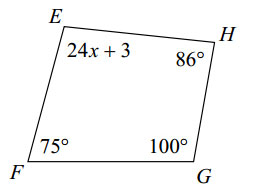
SOLUTION: Again, the object in question is a quadrilateral. If we add up all four angles in this quadrilateral, the sum will be \(360^\circ \). That is,
\(\left( {24x + 3} \right)^\circ + 86^\circ + 75^\circ + 100^\circ = 360^\circ \)
\(24x + 264^\circ = 360^\circ \),
\(24x = 96^\circ \)
\(x = 4^\circ \)
Below you can download some free math worksheets and practice.
Find the measure of each angle indicated.
This free worksheet contains 10 assignments each with 24 questions with answers.
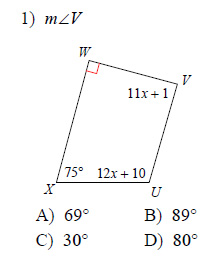
Example of one question:
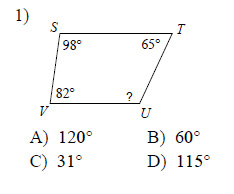
Watch below how to solve this example:
Solve for x.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
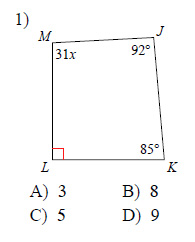
Watch below how to solve this example:
Find the measure of each angle indicated.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
Watch below how to solve this example:


